Welcome, this is the discussion board of TASVideos.
If you have a question, please read the Site FAQ first to see if your question has already been answered.
Be sure your posts conform to Site Rules
We also have a Discord server and an IRC channel #tasvideos at irc.libera.chat...
Be sure your posts conform to Site Rules
We also have a Discord server and an IRC channel #tasvideos at irc.libera.chat...





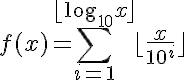 It may not look pretty but it's quite painless to calculate even for huge numbers as the number of summands grows verrrrry slowwwwwwly. Randil's solution is close but not quite right ... maybe ... depending on what you are actually asking.
It may not look pretty but it's quite painless to calculate even for huge numbers as the number of summands grows verrrrry slowwwwwwly. Randil's solution is close but not quite right ... maybe ... depending on what you are actually asking.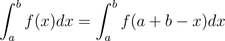 (b) Evaluate:
(b) Evaluate:

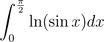 Come on, guys! You can do it!
Come on, guys! You can do it!







