Robomecha! (Level 28)
Algorithm and Part Optimization Walkthrough
The task: take an input string of only red and blue symbols and output an otherwise identical string with the last symbol moved to the front.
Generally I find Manufactoria levels to be easier if you try to come up with a basic algorithm on paper, which you bit by bit translate into Manufactoria-compatible components.
[Algorithm v1.0]
1. Read the last symbol
2. Move it to the front
Since we've all played the game a bit, we realize we can't just up and read the last symbol. Our tape is a LIFO stack. The only element on the tape we can read is the first one, by popping it off the stack. (It's also important to note the very act of positively identifying a symbol is destructive, which comes into play when we need to preserve some or all of the input.) The only way we can write an element to the tape is by pushing it onto the stack -- we can only append. This necessitates some modifications to our algorithm.
[Algorithm v2.0]
1. Transcribe symbols until the last one is reached.
2. Write the last symbol.
3. Transcribe the remainder of the string from the beginning again.
Though still very rough, we are starting to reach a point where we can translate our algorithm in to Manufactoria components. For example, we have a basic transcriber:

Of course, a R/B-only string will never leave such a device, so we use the trick of first marking the end of the input string with a different color:
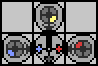
That's almost useful, but how do we know when we've reached the last symbol? Just a little ingenuity allows us to modify the transcriber to "record" the last symbol for us by having a separate branch for each option:
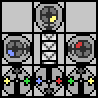
If the last symbol is blue, we head off to the left. If the last symbol is red, we head off to the right.
Now that we've modified the transcriber into something useful for our task, let's get back to the paper algorithm and refine it further.
[Algorithm v3.0]
1. Write Y to mark the end of the string.
Loop
2. Read R/B
3. Attempt to read Y
3a. Y: Exit loop and follow appropriate branch.
3b. Not Y: Write R/B and continue loop.
End Loop
Blue Branch
4. Write blue.
5. Transcribe the rest of the string.
Red Branch
4. Write red.
5. Transcribe the rest of the string.
Let's try to translate those branches back into Manufactoria:
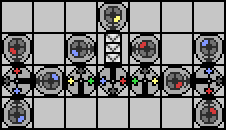
We run into a familiar problem with this naive attempt, namely we've forgotten we always need a way to exit a transcriber. We solved this problem last time by using a Y marker, let's try that again:
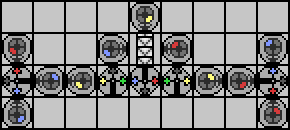
We're almost there! We've made all the needed modifications to the string, we'll just have a leftover yellow marker whenever the last transcription is done, or if the string is blank. Let's get rid of it:
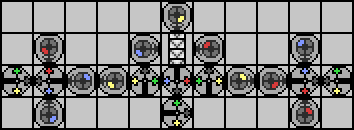
And that's it. This device will accept any R/B string, move the last symbol to the front, and have the string ready to be sent to the exit whenever the robot passes through any of the three downward pointing G/Y branches. For a task this simple it's pretty clear we probably can't do any better from an algorithmic standpoint. Can we reduce the number of parts we are using in Manufactoria, though?
One of the first things to look for when trying to reduce part usage is
duplicated components. Do we have any of those here? Well, we have three transcribers in our device. One of them is a special transcriber that recognizes the last component in a string, so we probably can't get rid of that one. The other two are just normal transcribers though. Do we really need both of them? Though we don't realize any immediate gains, let's use conveyors to get rid of one of the transcribers:
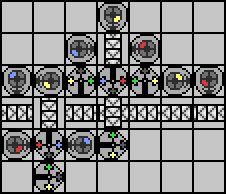
Another thing to look for when trying to reduce part usage is branches that allow for what I call "redundant passthrough." In the above picture we had to do some pretty ugly gymnastics with conveyors to allow for a blank string (which is actually one of the tests!) But let's think about what really happens when we get a blank string. It just goes straight down, failing to be redirected by any R/B branch. If that's the case, a blank string could pass through as many R/B branches as we wanted without issue. Why not send it through the second transcriber to get rid of some conveyors?
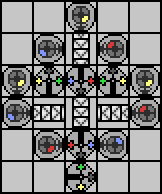
Now we're talking! That's starting to look really slick. Can we do
even better? Here's where we really need to start thinking outside the box. So far we've been stuck thinking about a transcriber as a device we enter through a R/B branch. But in truth you can enter any single part from any direction, and any multi-part component through any of its external pieces. What happens if we enter a transcriber through one of the writing parts? We end up writing an extra symbol of a particular color.
But wait ... isn't that what our algorithm is doing just before we go to the last transcription step? We write an extra symbol of a particular color, then transcribe the rest of the string. What if instead of explicitly writing the extra symbol, we let the transcriber do it by entering it from a different direction?
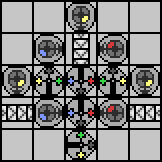
Wow! Add in to- and from-conveyors and we get the final, fully optimized solution:
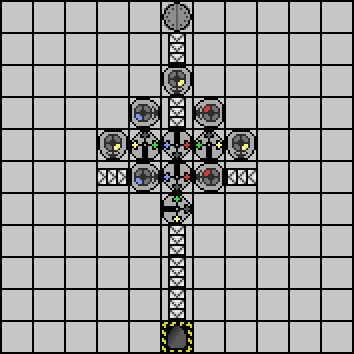
Or if you prefer the level code:
?lvl=28&code=c10:7f2;b11:5f2;b11:7f2;c12:5f3;p12:6f3;p12:7f3;r13:5f0;r13:7f0;c14:7f0;y12:4f3;y10:6f3;y14:6f3;q11:6f5;q13:6f1;q12:8f2;c12:3f3;c12:9f3;c12:10f3;c12:11f3;
I hope you folks found this informative. If you'd like me to make walkthroughs for any other levels, just ask. Most of my solutions are very well optimized, and I remember the steps I went through to get there.




 Apologies about the shoddy indents and row spacing; I tightened it a bit to make it fit on screen for a screenshot (which takes less visual space on the forums than a code paste does).
Apologies about the shoddy indents and row spacing; I tightened it a bit to make it fit on screen for a screenshot (which takes less visual space on the forums than a code paste does).

 I"m not a programmer, you see. I'm not used to make algorithms so this is being mostly intuitive play.
I"m not a programmer, you see. I'm not used to make algorithms so this is being mostly intuitive play. Of course, a R/B-only string will never leave such a device, so we use the trick of first marking the end of the input string with a different color:
Of course, a R/B-only string will never leave such a device, so we use the trick of first marking the end of the input string with a different color:
 That's almost useful, but how do we know when we've reached the last symbol? Just a little ingenuity allows us to modify the transcriber to "record" the last symbol for us by having a separate branch for each option:
That's almost useful, but how do we know when we've reached the last symbol? Just a little ingenuity allows us to modify the transcriber to "record" the last symbol for us by having a separate branch for each option:
 If the last symbol is blue, we head off to the left. If the last symbol is red, we head off to the right.
Now that we've modified the transcriber into something useful for our task, let's get back to the paper algorithm and refine it further.
If the last symbol is blue, we head off to the left. If the last symbol is red, we head off to the right.
Now that we've modified the transcriber into something useful for our task, let's get back to the paper algorithm and refine it further.
 We run into a familiar problem with this naive attempt, namely we've forgotten we always need a way to exit a transcriber. We solved this problem last time by using a Y marker, let's try that again:
We run into a familiar problem with this naive attempt, namely we've forgotten we always need a way to exit a transcriber. We solved this problem last time by using a Y marker, let's try that again:
 We're almost there! We've made all the needed modifications to the string, we'll just have a leftover yellow marker whenever the last transcription is done, or if the string is blank. Let's get rid of it:
We're almost there! We've made all the needed modifications to the string, we'll just have a leftover yellow marker whenever the last transcription is done, or if the string is blank. Let's get rid of it:
 And that's it. This device will accept any R/B string, move the last symbol to the front, and have the string ready to be sent to the exit whenever the robot passes through any of the three downward pointing G/Y branches. For a task this simple it's pretty clear we probably can't do any better from an algorithmic standpoint. Can we reduce the number of parts we are using in Manufactoria, though?
One of the first things to look for when trying to reduce part usage is duplicated components. Do we have any of those here? Well, we have three transcribers in our device. One of them is a special transcriber that recognizes the last component in a string, so we probably can't get rid of that one. The other two are just normal transcribers though. Do we really need both of them? Though we don't realize any immediate gains, let's use conveyors to get rid of one of the transcribers:
And that's it. This device will accept any R/B string, move the last symbol to the front, and have the string ready to be sent to the exit whenever the robot passes through any of the three downward pointing G/Y branches. For a task this simple it's pretty clear we probably can't do any better from an algorithmic standpoint. Can we reduce the number of parts we are using in Manufactoria, though?
One of the first things to look for when trying to reduce part usage is duplicated components. Do we have any of those here? Well, we have three transcribers in our device. One of them is a special transcriber that recognizes the last component in a string, so we probably can't get rid of that one. The other two are just normal transcribers though. Do we really need both of them? Though we don't realize any immediate gains, let's use conveyors to get rid of one of the transcribers:
 Another thing to look for when trying to reduce part usage is branches that allow for what I call "redundant passthrough." In the above picture we had to do some pretty ugly gymnastics with conveyors to allow for a blank string (which is actually one of the tests!) But let's think about what really happens when we get a blank string. It just goes straight down, failing to be redirected by any R/B branch. If that's the case, a blank string could pass through as many R/B branches as we wanted without issue. Why not send it through the second transcriber to get rid of some conveyors?
Another thing to look for when trying to reduce part usage is branches that allow for what I call "redundant passthrough." In the above picture we had to do some pretty ugly gymnastics with conveyors to allow for a blank string (which is actually one of the tests!) But let's think about what really happens when we get a blank string. It just goes straight down, failing to be redirected by any R/B branch. If that's the case, a blank string could pass through as many R/B branches as we wanted without issue. Why not send it through the second transcriber to get rid of some conveyors?
 Now we're talking! That's starting to look really slick. Can we do even better? Here's where we really need to start thinking outside the box. So far we've been stuck thinking about a transcriber as a device we enter through a R/B branch. But in truth you can enter any single part from any direction, and any multi-part component through any of its external pieces. What happens if we enter a transcriber through one of the writing parts? We end up writing an extra symbol of a particular color.
But wait ... isn't that what our algorithm is doing just before we go to the last transcription step? We write an extra symbol of a particular color, then transcribe the rest of the string. What if instead of explicitly writing the extra symbol, we let the transcriber do it by entering it from a different direction?
Now we're talking! That's starting to look really slick. Can we do even better? Here's where we really need to start thinking outside the box. So far we've been stuck thinking about a transcriber as a device we enter through a R/B branch. But in truth you can enter any single part from any direction, and any multi-part component through any of its external pieces. What happens if we enter a transcriber through one of the writing parts? We end up writing an extra symbol of a particular color.
But wait ... isn't that what our algorithm is doing just before we go to the last transcription step? We write an extra symbol of a particular color, then transcribe the rest of the string. What if instead of explicitly writing the extra symbol, we let the transcriber do it by entering it from a different direction?
 Wow! Add in to- and from-conveyors and we get the final, fully optimized solution:
Wow! Add in to- and from-conveyors and we get the final, fully optimized solution:
 Or if you prefer the level code:
Or if you prefer the level code:














