I thought it might be interesting to examine what other divisors F
mn have if we remove all of the divisors from F
m and F
n
3 : {"2": 1}
4 : {"3": 1}
5 : {"5": 1}
6 : {"2": 2}
7 : {"13": 1}
8 : {"7": 1}
9 : {"17": 1}
10 : {"11": 1}
11 : {"89": 1}
12 : {"2": 1, "3": 1}
13 : {"233": 1}
14 : {"29": 1}
15 : {"61": 1}
16 : {"47": 1}
17 : {"1597": 1}
18 : {"19": 1}
19 : {"37": 1, "113": 1}
20 : {"41": 1}
21 : {"421": 1}
22 : {"199": 1}
23 : {"28657": 1}
24 : {"2": 1, "23": 1}
25 : {"5": 1, "3001": 1}
26 : {"521": 1}
27 : {"53": 1, "109": 1}
28 : {"281": 1}
29 : {"514229": 1}
30 : {"31": 1}
31 : {"557": 1, "2417": 1}
32 : {"2207": 1}
33 : {"19801": 1}
34 : {"3571": 1}
35 : {"141961": 1}
36 : {"3": 1, "107": 1}
37 : {"73": 1, "149": 1, "2221": 1}
38 : {"9349": 1}
39 : {"135721": 1}
40 : {"2161": 1}
41 : {"2789": 1, "59369": 1}
42 : {"211": 1}
43 : {"433494437": 1}
44 : {"43": 1, "307": 1}
45 : {"109441": 1}
46 : {"139": 1, "461": 1}
47 : {"2971215073": 1}
48 : {"2": 1, "1103": 1}
49 : {"97": 1, "6168709": 1}
50 : {"101": 1, "151": 1}
51 : {"6376021": 1}
52 : {"90481": 1}
53 : {"953": 1, "55945741": 1}
54 : {"5779": 1}
55 : {"661": 1, "474541": 1}
56 : {"7": 1, "14503": 1}
57 : {"797": 1, "54833": 1}
58 : {"59": 1, "19489": 1}
59 : {"353": 1, "2710260697": 1}
60 : {"2521": 1}
61 : {"4513": 1, "555003497": 1}
62 : {"3010349": 1}
63 : {"35239681": 1}
64 : {"1087": 1, "4481": 1}
65 : {"14736206161": 1}
66 : {"9901": 1}
67 : {"269": 1, "116849": 1, "1429913": 1}
68 : {"67": 1, "63443": 1}
69 : {"137": 1, "829": 1, "18077": 1}
70 : {"71": 1, "911": 1}
71 : {"6673": 1, "46165371073": 1}
72 : {"103681": 1}
73 : {"9375829": 1, "86020717": 1}
74 : {"54018521": 1}
75 : {"230686501": 1}
76 : {"29134601": 1}
77 : {"988681": 1, "4832521": 1}
78 : {"79": 1, "859": 1}
79 : {"157": 1, "92180471494753": 1}
80 : {"1601": 1, "3041": 1}
81 : {"2269": 1, "4373": 1, "19441": 1}
82 : {"370248451": 1}
83 : {"99194853094755497": 1}
84 : {"83": 1, "1427": 1}
85 : {"9521": 1, "3415914041": 1}
86 : {"6709": 1, "144481": 1}
87 : {"173": 1, "3821263937": 1}
88 : {"263": 1, "881": 1, "967": 1}
89 : {"1069": 1, "1665088321800481": 1}
90 : {"181": 1, "541": 1}
91 : {"13": 1, "741469": 1, "159607993": 1}
92 : {"4969": 1, "275449": 1}
93 : {"4531100550901": 1}
94 : {"6643838879": 1}
95 : {"761": 1, "29641": 1, "67735001": 1}
96 : {"2": 1, "769": 1, "3167": 1}
97 : {"193": 1, "389": 1, "3084989": 1, "361040209": 1}
98 : {"599786069": 1}
99 : {"197": 1, "18546805133": 1}
100 : {"401": 1, "570601": 1}
101 : {"743519377": 1, "770857978613": 1}
102 : {"919": 1, "3469": 1}
103 : {"519121": 1, "5644193": 1, "512119709": 1}
104 : {"103": 1, "102193207": 1}
105 : {"8288823481": 1}
106 : {"119218851371": 1}
107 : {"1247833": 1, "8242065050061761": 1}
108 : {"3": 1, "11128427": 1}
109 : {"827728777": 1, "32529675488417": 1}
110 : {"11": 1, "331": 1, "39161": 1}
111 : {"1459000305513721": 1}
112 : {"10745088481": 1}
113 : {"677": 1, "272602401466814027129": 1}
114 : {"229": 1, "95419": 1}
115 : {"1381": 1, "2441738887963981": 1}
116 : {"347": 1, "1270083883": 1}
117 : {"29717": 1, "39589685693": 1}
118 : {"709": 1, "8969": 1, "336419": 1}
119 : {"159512939815855788121": 1}
120 : {"241": 1, "20641": 1}
121 : {"97415813466381445596089": 1}
122 : {"5600748293801": 1}
123 : {"68541957733949701": 1}
124 : {"3020733700601": 1}
125 : {"5": 1, "158414167964045700001": 1}
126 : {"1009": 1, "31249": 1}
127 : {"27941": 1, "5568053048227732210073": 1}
128 : {"127": 1, "186812208641": 1}
129 : {"257": 1, "5417": 1, "8513": 1, "39639893": 1}
130 : {"131": 1, "2081": 1, "24571": 1}
131 : {"1066340417491710595814572169": 1}
132 : {"261399601": 1}
133 : {"3457": 1, "42293": 1, "351301301942501": 1}
134 : {"4021": 1, "24994118449": 1}
135 : {"1114769954367361": 1}
136 : {"23230657239121": 1}
137 : {"19134702400093278081449423917": 1}
138 : {"691": 1, "1485571": 1}
139 : {"277": 1, "2114537501": 1, "85526722937689093": 1}
140 : {"12317523121": 1}
141 : {"108289": 1, "1435097": 1, "142017737": 1}
142 : {"688846502588399": 1}
143 : {"8581": 1, "1929584153756850496621": 1}
144 : {"10749957121": 1}
145 : {"349619996930737079890201": 1}
146 : {"151549": 1, "11899937029": 1}
147 : {"293": 1, "3529": 1, "347502052673": 1}
148 : {"11987": 1, "81143477963": 1}
149 : {"110557": 1, "162709": 1, "4000949": 1, "85607646594577": 1}
150 : {"12301": 1, "18451": 1}
151 : {"5737": 1, "2811666624525811646469915877": 1}
152 : {"1091346396980401": 1}
153 : {"17": 1, "7175323114950564593": 1}
154 : {"229769": 1, "9321929": 1}
155 : {"21701": 1, "12370533881": 1, "61182778621": 1}
156 : {"12280217041": 1}
157 : {"313": 1, "11617": 1, "7636481": 1, "10424204306491346737": 1}
158 : {"32361122672259149": 1}
159 : {"317": 1, "97639037": 1, "229602768949": 1}
160 : {"23725145626561": 1}
161 : {"8693": 1, "612606107755058997065597": 1}
162 : {"3079": 1, "62650261": 1}
163 : {"977": 1, "4892609": 1, "33365519393": 1, "32566223208133": 1}
164 : {"163": 1, "800483": 1, "350207569": 1}
165 : {"86461": 1, "518101": 1, "900241": 1}
166 : {"35761381": 1, "6202401259": 1}
167 : {"18104700793": 1, "1966344318693345608565721": 1}
168 : {"167": 1, "65740583": 1}
169 : {"337": 1, "89909": 1, "104600155609": 1, "126213229732669": 1}
170 : {"1158551": 1, "12760031": 1}
171 : {"6841": 1, "5741461760879844361": 1}
172 : {"313195711516578281": 1}
173 : {"1639343785721": 1, "389678749007629271532733": 1}
174 : {"349": 1, "947104099": 1}
175 : {"701": 1, "17231203730201189308301": 1}
176 : {"93058241": 1, "562418561": 1}
177 : {"2191261": 1, "805134061": 1, "1297027681": 1}
178 : {"179": 1, "22235502640988369": 1}
179 : {"21481": 1, "156089": 1, "3418816640903898929534613769": 1}
180 : {"10783342081": 1}
181 : {"8689": 1, "422453": 1, "8175789237238547574551461093": 1}
182 : {"689667151970161": 1}
183 : {"1097": 1, "14297347971975757800833": 1}
184 : {"253367": 1, "9506372193863": 1}
185 : {"1702945513191305556907097618161": 1}
186 : {"63799": 1, "35510749": 1}
187 : {"373": 1, "10157807305963434099105034917037": 1}
188 : {"563": 1, "5641": 1, "4632894751907": 1}
189 : {"38933": 1, "955921950316735037": 1}
190 : {"191": 1, "41611": 1, "87382901": 1}
191 : {"4870723671313": 1, "757810806256989128439975793": 1}
192 : {"2": 1, "11862575248703": 1}
193 : {"9465278929": 1, "1020930432032326933976826008497": 1}
194 : {"3299": 1, "56678557502141579": 1}
195 : {"88999250837499877681": 1}
196 : {"5881": 1, "61025309469041": 1}
197 : {"15761": 1, "25795969": 1, "227150265697": 1, "717185107125886549": 1}
198 : {"991": 1, "2179": 1, "1513909": 1}
199 : {"397": 1, "436782169201002048261171378550055269633": 1}
200 : {"9125201": 1, "5738108801": 1}
201 : {"5050260704396247169315999021": 1}
202 : {"809": 1, "7879": 1, "201062946718741": 1}
203 : {"1217": 1, "56470541": 1, "2586982700656733994659533": 1}
204 : {"409": 1, "66265118449": 1}
205 : {"821": 1, "125598581": 1, "36448117857891321536401": 1}
206 : {"619": 1, "1031": 1, "5257480026438961": 1}
207 : {"4072353155773627601222196481": 1}
208 : {"3329": 1, "106513889": 1, "325759201": 1}
209 : {"57314120955051297736679165379998262001": 1}
210 : {"21211": 1, "767131": 1}
211 : {"22504837": 1, "38490197": 1, "800972881": 1, "80475423858449593021": 1}
212 : {"1483": 1, "2969": 1, "1076012367720403": 1}
213 : {"1277": 1, "185790722054921374395775013": 1}
214 : {"47927441": 1, "479836483312919": 1}
215 : {"2607553541": 1, "67712817361580804952011621": 1}
216 : {"6263": 1, "177962167367": 1}
217 : {"433": 1, "44269": 1, "217221773": 1, "2191174861": 1, "6274653314021": 1}
218 : {"128621": 1, "788071": 1, "593985111211": 1}
219 : {"123953": 1, "4139537": 1, "3169251245945843761": 1}
220 : {"59996854928656801": 1}
221 : {"203572412497": 1, "90657498718024645326392940193": 1}
222 : {"4441": 1, "146521": 1, "1121101": 1}
223 : {"4013": 1, "108377": 1, "251534189": 1, "164344610046410138896156070813": 1}
224 : {"223": 1, "449": 1, "1154149773784223": 1}
225 : {"11981661982050957053616001": 1}
226 : {"412670427844921037470771": 1}
227 : {"23609": 1, "5219534137983025159078847113619467285727377": 1}
228 : {"227": 1, "26449": 1, "212067587": 1}
229 : {"457": 1, "2749": 1, "40487201": 1, "132605449901": 1, "47831560297620361798553": 1}
230 : {"1151": 1, "5981": 1, "324301": 1, "686551": 1}
231 : {"9164259601748159235188401": 1}
232 : {"299281": 1, "834428410879506721": 1}
I dunno. There do seem to be more very large primes than I expected.
Something I found surprising while writing this program. F
m2 is divisible by F
m but not necessarily by F
m2. The first counter example is F
9.





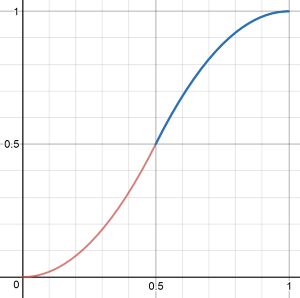 With an exponent of 4 the curve is more pronounced:
With an exponent of 4 the curve is more pronounced:
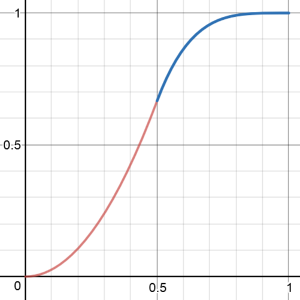
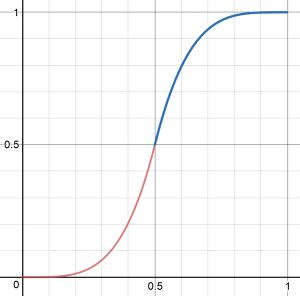 The important thing is that the curve is smooth over the entire range.
Now, what if we wanted the starting acceleration to be less pronounced than the ending deceleration? In other words, what if we wanted to use two exponents rather than one: The first exponent for the first half, and the second exponent for the second half. We can't simply plug the two exponents in the above code because the resulting curve is not smooth:
The important thing is that the curve is smooth over the entire range.
Now, what if we wanted the starting acceleration to be less pronounced than the ending deceleration? In other words, what if we wanted to use two exponents rather than one: The first exponent for the first half, and the second exponent for the second half. We can't simply plug the two exponents in the above code because the resulting curve is not smooth:
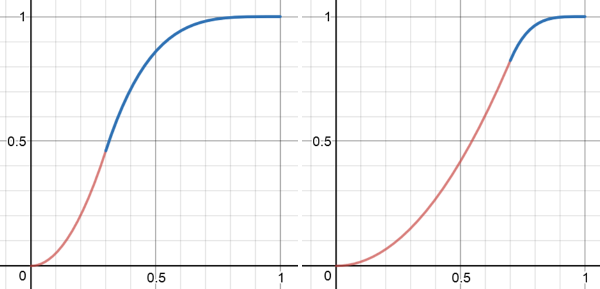
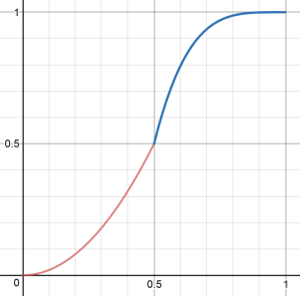 There's a visible jump in slope at t=0.5 (and this jump becomes very obvious if eg. used in an animation).
So my question is: How to get a smooth curve like this, where the starting half uses one exponent and the ending half uses another?
One possibility would be to change those 0.5 factors in the formula, so that the joint point at t=0.5 goes up or down (in this example it would have to go up). But by how much, exactly?
There's a visible jump in slope at t=0.5 (and this jump becomes very obvious if eg. used in an animation).
So my question is: How to get a smooth curve like this, where the starting half uses one exponent and the ending half uses another?
One possibility would be to change those 0.5 factors in the formula, so that the joint point at t=0.5 goes up or down (in this example it would have to go up). But by how much, exactly?