I think I got it, although I don't know if there is a simpler way to do this:
f(xy) gcd(f(x), y) = f(x) f(y) and f(yx) gcd(f(y), x) = f(y) f(x) imply gcd(f(x),y) = gcd(f(y),x) for all x,y.
Two important properties:
[1] If we let f(x)=n, then n=gcd(f(x),n)=gcd(f(n),x) implying n divides x (notation: n|x). That is, f(x)|x for all x.
[2] Note that gcd(f(x),y)|y and gcd(f(y),x)|x. If gcd(x,y)=1, it follows that gcd(f(x),y)=gcd(f(y),x)=1. Then f(xy) gcd(f(x), y) = f(x) f(y) becomes f(xy) = f(x) f(y). Therefore f(x) must be a
multiplicative function.
Now we check specific values. First, by property [1], f(1) must be 1.
Then we check f(p) for prime p. By property [1], f(p) is either 1 or p:
Case 1: f(p)=1. Then x=y=p gives f(p
2) gcd(f(p),p) = f(p)f(p) ---> f(p
2)=1. Likewise, x=p
2, y=p gives f(p
3)=1, and so on. By induction, f(p
n)=1.
Case 2: f(p)=p. Then x=y=p gives f(p
2) gcd(f(p),p) = f(p)f(p) ---> f(p
2)=p. Likewise, x=p
2, y=p gives f(p
3)=p, and so on. By induction, f(p
n)=p.
Thus, for each prime p, we have a choice whether to assign f(p
n)=1 for all n≥1, or f(p
n)=p for all n≥1; that is, whether to include p as a prime factor in the output or not. Together with with the multiplicative function property [2], we can summarize possible f as follows: Any function satisfying f(xy) gcd(f(x), y) = f(x) f(y) must be of the form f
Q(x), where Q is a (possibly infinite) subset of the primes, and f
Q(x) is the product of all prime factors of x that are in Q.
----
There is one other thing: The above reasoning does not actually verify that f=f
Q(x) satisfies the equation. To verify it, we need one more thing:
Consider a function f=f
Q(x). To check that f
Q(xy) gcd(f
Q(x), y) = f
Q(x) f
Q(y), we will look at each prime p:
Case 1: p is not in Q: None of the factors in the equation will contain the factor p then.
Case 2: p is in Q but divides neither x nor y: None of the factors in the equation will contain the factor p then.
Case 3: p is in Q and divides x, but not y: The factors f
Q(xy) and f
Q(x) will each contain exactly one factor of p, and only these factors.
Case 4: p is in Q and divides y, but not x: The factors f
Q(xy) and f
Q(y) will each contain exactly one factor of p, and only these factors.
Case 5: p is in Q and divides both x and y: The factors f
Q(xy), gcd(f
Q(x), y), f
Q(x) and f
Q(y) will each contain exactly one factor of p.
In all cases, the factors of p are balanced on both sides. Doing this over all primes p shows that the equation holds.






 So the equation (x2-3x-3)ex - m = 0 has:
So the equation (x2-3x-3)ex - m = 0 has:
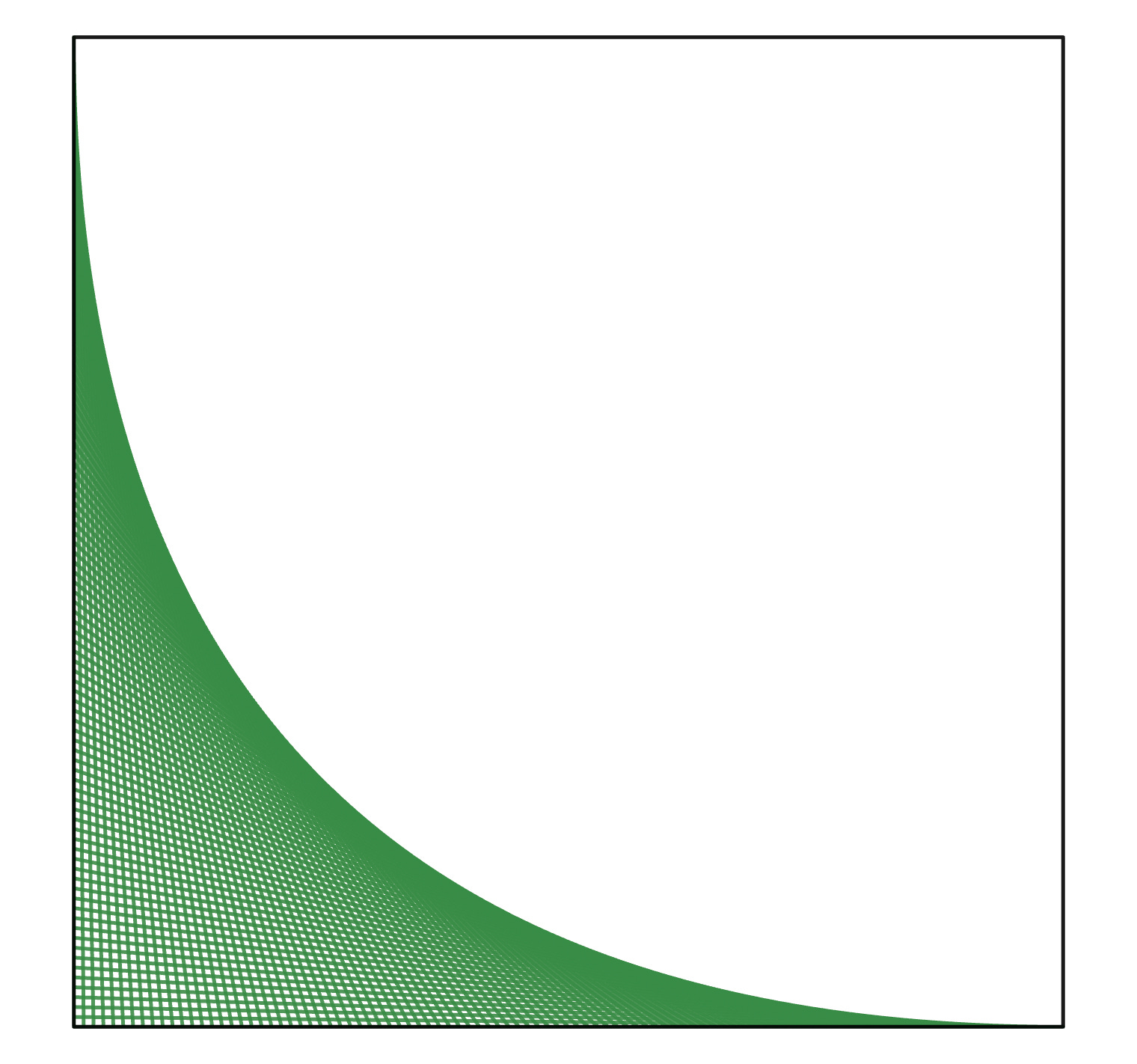 We form a weaving loom pattern in the unit square as follows:
* On the left side from the top-left corner to the bottom-left corner are n equally-spaced points A1, A2, ..., An.
* On the bottom side from the bottom-left corner to the bottom-right corner are n equally-spaced points B1, B2, ..., Bn. Note that B1 = An.
* Draw n line segments: from A1 to B1, A2 to B2, and so on, up to An to Bn.
The figure above shows n=100.
Question: As n goes to infinity, what is the curve formed by the upper edge of the pattern?
----
Fiddler on the proof also has a bonus question ("Extra Credit"). Rotate the above pattern around so it looks like this:
We form a weaving loom pattern in the unit square as follows:
* On the left side from the top-left corner to the bottom-left corner are n equally-spaced points A1, A2, ..., An.
* On the bottom side from the bottom-left corner to the bottom-right corner are n equally-spaced points B1, B2, ..., Bn. Note that B1 = An.
* Draw n line segments: from A1 to B1, A2 to B2, and so on, up to An to Bn.
The figure above shows n=100.
Question: As n goes to infinity, what is the curve formed by the upper edge of the pattern?
----
Fiddler on the proof also has a bonus question ("Extra Credit"). Rotate the above pattern around so it looks like this:
 Question: As n goes to infinity, what fraction of the unit square is not covered by the four patterns (that is, what is the area of the central white region)?
Question: As n goes to infinity, what fraction of the unit square is not covered by the four patterns (that is, what is the area of the central white region)?