Posted: 6/25/2006 7:25 AM
Post subject: Tetris math question
Quote
Ramzi
Joined: 3/25/2004
Posts: 459
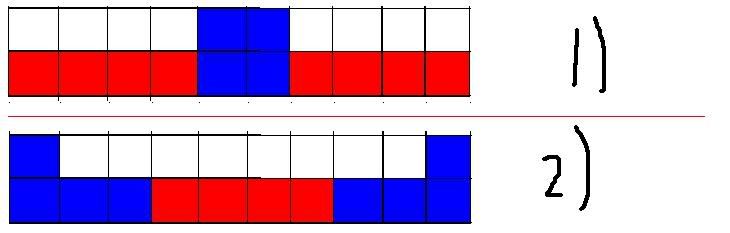Suppose I wrote a Tetris computer program that left piece-objects in memory until they were completed removed from the board. What is the maximum number of piece-objects I can have in memory? In the first diagram, after the line breaks, I would have one piece object still in memory. In the second diagram, after the line breaks, I would have two piece object still in memory. To get the most objects, we would want most pieces to break down and occupy only 1 cell. This becomes difficult at the top of the board. Also, how does having or not having gravity affect the answer to the question?
Posted: 6/25/2006 8:06 AM
Quote
Blublu
Player (68)
Joined: 3/11/2004
Posts: 1058
Location: Reykjaví­k, Ísland
Well, I would think to get the theoretical maximum, all you have to do is multiply the number of rows and the number of comumns, then subtract the number of rows. For example: (( 10 * 20 ) - 20 ) = 180 Of course, if you can't reach the upper corners properly it gets more complicated...
Posted: 6/25/2006 8:20 AM
Quote
upthorn
He/Him
Emulator Coder, Active player (392)
Joined: 3/24/2006
Posts: 1802
Sega TAS of 2011 Sega TAS of 2010 Sega TAS of 2008 Sega TASer of 2007
The problem with that number is that It becomes not just difficult, but impossible to reduce pieces to a single cell near the top.
How fleeting are all human passions compared with the massive continuity of ducks.
Posted: 6/25/2006 9:09 AM
Quote
Blublu
Player (68)
Joined: 3/11/2004
Posts: 1058
Location: Reykjaví­k, Ísland
Oh yeah, I didn't think of that. Well then I have no idea. :P
Posted: 6/25/2006 6:38 PM
Quote
Ramzi
Joined: 3/25/2004
Posts: 459
Actually, I don't really care too much about the top because there are so many different rules to govern it. For example, in some games, if the piece your set is over the top barrier, but it breaks a line, the line will break, and the game will continue. Others won't break that line. Also, some games always have the piece come from the center, and other games let you begin moving it beforehand. But can we say we confidence, that, assuming an infinite Height (capital), we can achieve single pieces to make up [(width*height)-height] for an arbitrary height, like half of a standard board?
Posted: 6/25/2006 7:25 PM
Quote
Tub
Joined: 6/25/2005
Posts: 1377
Let's look for a tactic, that'll allow us to return to a previous pattern, in this case a clean floor with one hole in it. Then we'll have a sequence of insertions, that can be repeated over and over - not reaching any arbitrary height, but at least multiples of our sequence. every piece is 4 fields big. we'll look for a sequence generating h new rows. if every field should contain only one piece, at least h * (width-1) pieces have to be used to create this pattern. so, h*(width-1)*3 fields were removed. This number has to be divisible by width, otherwise that weren't full lines. this doesn't prove that such a tactic exists, it just proves that you'll need different tactics for different board widths, if you're relying on repeating sequences. in other words: the proof is going to be much more complicated than just finding a generic working strategy.
m00
Posted: 6/25/2006 9:35 PM
Quote
Ramzi
Joined: 3/25/2004
Posts: 459
I guess let's work with a standard width of 10, since that's what all Tetris games use. Is it possible to create 1 line with 9 piece objects, and then replicate that strategy again?
Posted: 6/25/2006 10:28 PM
Quote
Tub
Joined: 6/25/2005
Posts: 1377
no, see my previous post. If you count pieces, you can only add multiples of 4 to the board, and only remove multiples of 10. When starting with an empty board, you'll never have 9 pieces left over. try finding a sequence that leaves an even number of rows with 9 1-piece objects, preferably 2. Be advised though, that you can't achieve this with just 18 pieces, you'll need more. You'll need at least 4 extra pieces that'll be completely removed by finished lines, or any multiple of 5 more (e.g. 9, 14, 19, ...). This still doesn't prove that it's possible, it just rules out some ways that can't succeed.
m00
Posted: 6/25/2006 11:30 PM
Quote
JXQ
Experienced player (761)
Joined: 5/6/2005
Posts: 3132
NES TAS of 2008 Speedy TAS of 2008 SNES TASer of 2007 TAS of 2007 SNES TAS of 2007 Funny TAS of 2007
This may be ugly, but... 

      4
      4
1112224333
1  2  43

----------
                              
      4
5556664777
15 26 437

----------

         0
8889994000
158269437

----------

         0
158269437

----------
         
      D
      D
AAABBBDCCC
  AB  DC 0
158269437

----------

      D
EEEFFFDGGG
 EABF DCG0
158269437

----------

I        J
IIIHHHDJJJ
 EABFHDCG0
158269437

----------


IKKKKLLLLJ
 EABFHDCG0
158269437

----------

 EABFHDCG0
158269437
The highest this makes the stack is three higher than the pile (piece D), and if that is placed last, then it may not matter, depending on how the rules go above the top of the board. Lather, rinse, repeat. EDIT: Hmm, you can't repeat it verbatum, because piece 1 will fit into the hole on the second row. So instead, use a mirror image of the above algorithm for the second repetition, and then the original for the third, etc.
<Swordless> Go hug a tree, you vegetarian (I bet you really are one)
Posted: 6/26/2006 12:41 AM
Quote
Ramzi
Joined: 3/25/2004
Posts: 459
Wow, very impressive JXQ. This is without gravity. See in frame 4, if there was gravity, that 0 would fall, and break the last line. I'm pretty sure I solved it with gravity last night at 3am, when I posted this, but I don't remember.
Posted: 6/26/2006 12:52 AM
Quote
Tub
Joined: 6/25/2005
Posts: 1377 
123456789
123456789
123456789
123456789

AAAABBBB00
1234567890
1234567890
123456789
123456789

C
CCCDDDDEEE
123456789E
123456789

 FGHIJKLMN
 FGHIJKLMN
 FGHIJKLMN
CDEFGHIJMN
123456789

OOPPPPQQQQ
ODEFGHIJKL
ODEFGHIJKL
 DEFGHIJKL
123456789

 DEFGHIJKL
123456789
mirror, repeat. As predicted, 9 additional pieces were used and completely removed (0 to E and O to Q)
m00
Posted: 6/27/2006 12:35 AM
Quote
flagitious
Player (201)
Joined: 7/6/2004
Posts: 511 
12345678
123456789
1234567899
123456789

        0
1234567800
1234567890
123456789

kkkklllljj
abcdefghjj
abcdefghii
abcdefghii
abcdefgh0
123456789

abcdefgh0
123456789
Here's a way that only uses 4 extra (gravity independent too), not that this of any use as you already proved the point, I was just bored.
g,o,p,i=1e4,a[10001];main(x){for(;p?g=g/x*p+a[p]*i+2*!o: 53^(printf("%.4d",o+g/i),p=i,o=g%i);a[p--]=g%x)x=p*2-1;}
Posted: 6/27/2006 5:38 AM
Quote
Xkeeper
Banned User
Joined: 12/23/2004
Posts: 1850
Tub wrote:
 FGHIJKLMN
 FGHIJKLMN
 FGHIJKLMN
CDEFGHIJMN
123456789
i think we have a porblem Piece N can't float over nothing.
Perma-banned
Posted: 6/27/2006 11:28 AM
Quote
jimsfriend
Former player
Joined: 1/17/2006
Posts: 775
Location: Deign
To fix that he could place N before D, I think. I can't really follow his example.
Deign Deign Deign Deign Deign Deign Deign Deign Deign Deign Deign Deign Deign Deign Deign Deign Deign Deign Deign Deign Deign Deign Deign Deign Deign Deign aqfaq Deign Deign Deign Deign Deign Deign Deign Deign Deign Deign Deign Deign Deign Deign Deign
Posted: 6/27/2006 11:39 AM
Quote
Tub
Joined: 6/25/2005
Posts: 1377
whoops, you're right, screw my tactic. But flagitious has the solution, so I won't bother fixing my way.
m00
Posted: 6/27/2006 5:58 PM
Post subject: demo
Quote
Xkeeper
Banned User
Joined: 12/23/2004
Posts: 1850
Also shows an alternate way of starting...
Perma-banned
Posted: 6/27/2006 7:24 PM
Quote
Ramzi
Joined: 3/25/2004
Posts: 459
While the animation is very nice and easy to follow... the bottom row is still only two pieces. JXQ's solution let's the bottom row be nice different pieces.
Posted: 6/27/2006 7:58 PM
Quote
trazz
Player (95)
Joined: 6/25/2005
Posts: 122
Ramzi wrote:
While the animation is very nice and easy to follow... the bottom row is still only two pieces. JXQ's solution let's the bottom row be nice different pieces.
No, the bottom row is comprised of the maximum number of pieces. The eight rows on the left can be made by eight "beanpole" pieces stacked like this: |||||||| The next piece completes three lines, leaving only the bottommost box of the eight beanpoles intact as well as adding a ninth box from the dropped piece.
Posted: 6/27/2006 8:12 PM
Quote
Ramzi
Joined: 3/25/2004
Posts: 459
Hahaha. I'm so dumb. For some reason I just thought they were placed horizontally, rather than vertically.
Posted: 6/28/2006 5:17 AM
Quote
Xkeeper
Banned User
Joined: 12/23/2004
Posts: 1850
If anyone else wants different demos, please let me know :)
Perma-banned
Posted: 6/28/2006 3:43 PM
Quote
Ramzi
Joined: 3/25/2004
Posts: 459
Is there a way to do this while maintaing the four-color theorem? That is, using only four colors for the tetris pieces, can you make the rows of 9 unique pieces without setting a piece down that shares a border with another piece of the same color?