Found the source code for the hilbert curves \o/
Many geeks know the
Hilbert curve. Not so many know that it can be extended into 3d space and beyond. In 2D space, the hilbert curve is unique (when the start- and end-corner are given), while in 3 or more dimensions, it is not. For the following, I picked a 3d curve that was experimentally chosen to provide the best spacial locality.
Exhibit 1:
I've defined a total order over the RGB-cube by said 3D hilbert curve, then laid out the colors line by line in ascending order.
TC_linear.png, 440 kB
The main property of hilbert curve is easy to see: there are no more "jumps". Each pixel is at most 1 color value away from the pixel to its left (or to the last pixel in the preceeding line).
While it is ordered, it doesn't look like a rainbow at all. Similar colors may appear at very different parts of the image. This is an unavoidable consequence of mapping a 3D space to a 1D space. (A rainbow will only display a 1D color space, fully saturated colors at equal brightness, just with different hue.)
Unlike arflech's slice-mapping, this attempt provided perfect locality to the pixels to the left and right, but not necessarily to the pixels above or below. After all, I did map to a 1D-space, in which colors 4096 positions apart are totally unrelated. Which leads me to
Exhibit 2:
Instead of laying out the ordered colors line by line, I've arranged them along a 2-dimensional hilbert curve.
TC_hilbert.png, 2.9 MB
At first glance, you'll see 16 cubes, each having roughly a similar tone. Zooming in, you'll notice smaller and smaller cubes. The smaller the cube, the smoother its color will be, so much that the 16x16 cubes look single-colored to the naked eye, despite showing 256 unique colors each.
/edit: replaced images with pngcrush'ed versions


 .
Edit:
.
Edit:






 [/thread]
[/thread]



 Here is a 16x16 pixel Kirby I made a few years ago for a Super Mario World hack I was working on (which involved Kirby). The checkerboard background helped me plot each pixel in my graphics editor. Looking back on the hack, it was too easy and the level design was really juvenile so I probably won't finish it.
I made it by studying this Kirby hi sprite from Kirby Tilt 'n' Tumble:
Here is a 16x16 pixel Kirby I made a few years ago for a Super Mario World hack I was working on (which involved Kirby). The checkerboard background helped me plot each pixel in my graphics editor. Looking back on the hack, it was too easy and the level design was really juvenile so I probably won't finish it.
I made it by studying this Kirby hi sprite from Kirby Tilt 'n' Tumble:
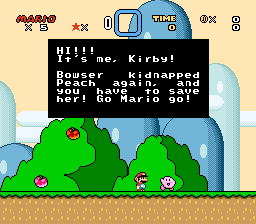
 Here's how it looked in-game:
Here's how it looked in-game: