To finish the question thatguy asked:
The first few values of the rows are as follows:
1 3 4 6 8 9 11 12 14 16 17 19 21...
2 5 7 10 13 15 18 20 23 26 28 31 34...
We let a
n be the nth value of the first row, and b
n be the nth value of the second row. [x] is the floor function, the smallest integer less than or equal to x.
In fact, these rows are a special case of a more general property as follows:
Given an irrational number α>1, there exists an irrational number β>1 (in particular, β=α/(α-1)) such that [n*α] and [n*β] partition the set of natural numbers {1,2,... }.
There are many proofs of this (as can be seen from the [url=
https://en.wikipedia.org/wiki/Beatty_sequence]Wikipedia page on Beatty sequences[/url]) but there is a geometric proof by taking a grid and drawing a line of slope α-1 through (0,0), as shown below:
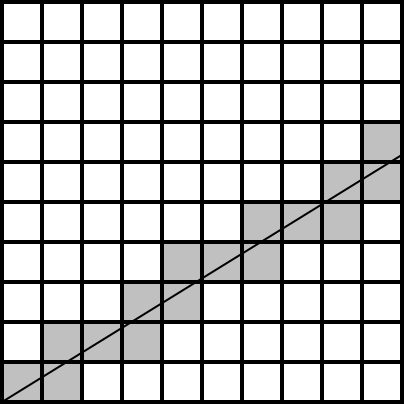
Note that, since α is irrational, the line does not pass through an intersection point of the grid other than (0,0). The gray squares (the ones which contain any part of this line) form a cell path from the bottom-left up and to the right. The kth step of this path is a rightward step if k is of the form n+[n*(α-1)]=[n*α]. By reflecting the diagram about y=x, it follows that the kth step is an upward step if k is of the form n+[n/(α-1)]=[n*(α/(α-1))]=[n*β]. Since there are only upward and rightward steps, [n*α] and [n*β] partition the set {1,2,... }.
(There is a way to allow α to be a rational number, but one of the floor functions has to be replaced with a modified floor function, the smallest integer strictly less than x.)
For example, the image above uses a line of slope φ-1, and the kth step is a rightward step if k is any one of the values a
n (1,3,4,6,8,9,... ), and an upward step if k is any one of the b
n (2,5,7,10,13,15,... ).
Letting α=φ gives (after some calculation) β=α/(α-1)=φ+1. (Note: Solving x+1=x/(x-1), x>1 gives φ as the only solution.) Therefore a
n=[n*φ], b
n=[n*(φ+1)]=n+[n*φ], and b
n-a
n=n.
Note that the rows can also be generated by recursively letting a
n be the smallest number not yet listed, then b
n=a
n+n. (There is only one way to place all natural numbers exactly once in two ascending rows {a
n} and {b
n} where b
n-a
n=n.) This ties into, for example, the
winning positions of Wythoff's game; the winning positions are (0,0), and (a
n,b
n) and (b
n,a
n) for all n.
 From this, we can determine the arc-length along the cross-section. What is the surface area on, say, one square-centimeter of small intestine? (By which I mean one centimeter by one centimeter punched out of the small intestines. The one square-centimeter measurement is macroscopic while the surface area I'm asking for comes from adding up all the microscopic ridges and folds and should therefore be much larger.)
I am almost certain the conversion factor should be proportional to the square of the arc-length divided by the horizontal distance spanned. Perhaps the proportionality constant is just one. Can anyone succinctly prove what it should be?
From this, we can determine the arc-length along the cross-section. What is the surface area on, say, one square-centimeter of small intestine? (By which I mean one centimeter by one centimeter punched out of the small intestines. The one square-centimeter measurement is macroscopic while the surface area I'm asking for comes from adding up all the microscopic ridges and folds and should therefore be much larger.)
I am almost certain the conversion factor should be proportional to the square of the arc-length divided by the horizontal distance spanned. Perhaps the proportionality constant is just one. Can anyone succinctly prove what it should be?









 Note that, since α is irrational, the line does not pass through an intersection point of the grid other than (0,0). The gray squares (the ones which contain any part of this line) form a cell path from the bottom-left up and to the right. The kth step of this path is a rightward step if k is of the form n+[n*(α-1)]=[n*α]. By reflecting the diagram about y=x, it follows that the kth step is an upward step if k is of the form n+[n/(α-1)]=[n*(α/(α-1))]=[n*β]. Since there are only upward and rightward steps, [n*α] and [n*β] partition the set {1,2,... }.
(There is a way to allow α to be a rational number, but one of the floor functions has to be replaced with a modified floor function, the smallest integer strictly less than x.)
For example, the image above uses a line of slope φ-1, and the kth step is a rightward step if k is any one of the values an (1,3,4,6,8,9,... ), and an upward step if k is any one of the bn (2,5,7,10,13,15,... ).
Letting α=φ gives (after some calculation) β=α/(α-1)=φ+1. (Note: Solving x+1=x/(x-1), x>1 gives φ as the only solution.) Therefore an=[n*φ], bn=[n*(φ+1)]=n+[n*φ], and bn-an=n.
Note that the rows can also be generated by recursively letting an be the smallest number not yet listed, then bn=an+n. (There is only one way to place all natural numbers exactly once in two ascending rows {an} and {bn} where bn-an=n.) This ties into, for example, the
Note that, since α is irrational, the line does not pass through an intersection point of the grid other than (0,0). The gray squares (the ones which contain any part of this line) form a cell path from the bottom-left up and to the right. The kth step of this path is a rightward step if k is of the form n+[n*(α-1)]=[n*α]. By reflecting the diagram about y=x, it follows that the kth step is an upward step if k is of the form n+[n/(α-1)]=[n*(α/(α-1))]=[n*β]. Since there are only upward and rightward steps, [n*α] and [n*β] partition the set {1,2,... }.
(There is a way to allow α to be a rational number, but one of the floor functions has to be replaced with a modified floor function, the smallest integer strictly less than x.)
For example, the image above uses a line of slope φ-1, and the kth step is a rightward step if k is any one of the values an (1,3,4,6,8,9,... ), and an upward step if k is any one of the bn (2,5,7,10,13,15,... ).
Letting α=φ gives (after some calculation) β=α/(α-1)=φ+1. (Note: Solving x+1=x/(x-1), x>1 gives φ as the only solution.) Therefore an=[n*φ], bn=[n*(φ+1)]=n+[n*φ], and bn-an=n.
Note that the rows can also be generated by recursively letting an be the smallest number not yet listed, then bn=an+n. (There is only one way to place all natural numbers exactly once in two ascending rows {an} and {bn} where bn-an=n.) This ties into, for example, the 














