That's a good one Warp.
Let's talk about matrix eigenvalue decomposition!
So it is possible to represent both the Fibonnaci and Lucas recurrence relation as the same matrix with different initial conditions.
This is to say, if you have a state vector (F
n-1, F
n) you can multiply it by a matrix to get the next state vector (F
n, F
n + 1)
Our initial vector for Fibonacci numbers is (0, 1). For Lucas numbers it's (2, 1).
Note: It seems that the limit you're computing is L
n / F
n+1 according to the canonical numbering.
So the formula for the vector containing the (n-1)th and nth Fibonacci number is (0, 1) * ( ( 0, 1 ), ( 1, 1) )
n
But computing the nth power of a matrix is hard. So we need to find a better way.
To begin, the matrix is simply:
A = ( ( 0, 1 ),
( 1, 1) )
Next, we calculate the eigenvalues of this matrix:
( ( 0-y, 1 ),
( 1, 1-y) )
(1-y)(-y) - 1 = 0
y
2 - y - 1 = 0
y
1 = (1 + sqrt(5))/2
y
2 = (1 - sqrt(5))/2
(Note: this is the underlying mathematical reason that both the Fibonacci and Lucas sequence ratios approach the golden ratio as n goes to infinity.)
So now that we have the eigenvalues we want to change the representation of the matrix from A into Q Y Q
-1, where Y is just the matrix with the eigenvalues down the diagonal. We want to do this because then we can raise this to the nth power easily.
(A
n is hard to calculate because it means lots of matrix multiplication. On the other hand, (Q Y Q
-1)
n is easy because the Q
-1 and Q cancel and we're left with Q Y
n Q
-1. Because Y is a diagonal matrix, it is simple to calculate the nth power of, you just compute the nth power of each diagonal member.)
It can be shown with a proof that Q must be the eigenvectors of A, but I'll omit that for brevity. Maybe this can be my challenge to you.
So to calculate the eigenvectors of A we just solve the system (A - yI) v = 0 for v. I'll spare the calculations because they're pretty much trivial we get:
v
1 = (-y
2, 1)
v
2 = (-y
1, 1)
So Q becomes:
( ( -y
2, -y
1 ),
( 1, 1) )
And Q
-1 is computed just by taking the inverse of Q:
( ( 1/sqrt(5), (1 + sqrt(5))/(2 sqrt(5)) ),
( -(1/sqrt(5)), (-1 + sqrt(5))/(2 sqrt(5)) ) )
Now we can use this to find an explicit formula for the nth Fibonacci (and Lucas) number. It's just:
(0, 1) Q Y
n Q
-1
And because we just care about a single value we can simplify it to a single formula:
(-(1/2 (1 - sqrt(5)))^n + (1/2 (1 + sqrt(5)))^n)/sqrt(5)
Which is the famous explicit formula for the Fibonacci sequence.
Similarly you can use the initial vector for the Lucas sequence to find the explicit formula for that. It is:
-2 + (1/2 (1 - sqrt(5)))^n + (1/2 (1 + sqrt(5)))^n
Because the limit you're looking for is L
n / F
n+1 we have:
(-2 + (1/2 (1 - sqrt(5)))^n + (1/2 (1 + sqrt(5)))^n) / ((-(1/2 (1 - sqrt(5)))^(n+1) + (1/2 (1 + sqrt(5)))^(n+1))/sqrt(5))
Which is messy looking but as n approaches infinity is:
1/2 ( 5 - sqrt(5) )
For L
n / F
n the formula is:
(-2 + (1/2 (1 - sqrt(5)))^n + (1/2 (1 + sqrt(5)))^n) / ((-(1/2 (1 - sqrt(5)))^n + (1/2 (1 + sqrt(5)))^n)/sqrt(5))
And the limit is simply:
sqrt(5)
Which is a lot nicer. :)




















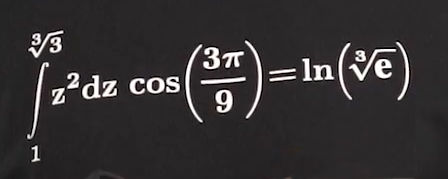 Is that really so?
Is that really so?





















